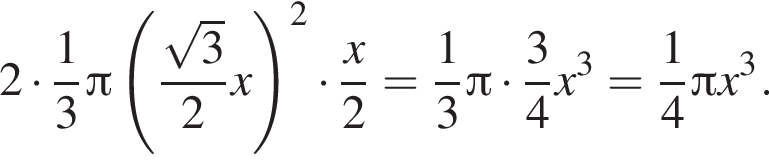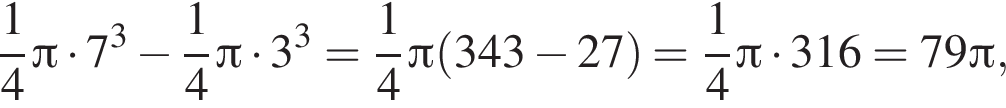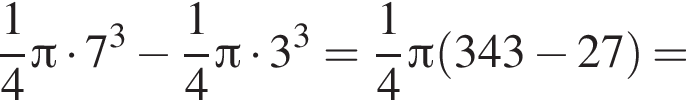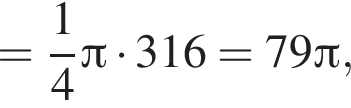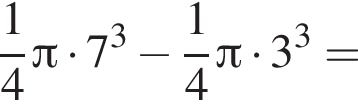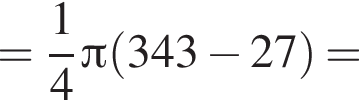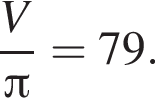Треугольник ABC — равнобедренный с основанием AB. Используя данные рисунка, найдите градусную меру угла BAC треугольника ABC.
Пусть O и O1 — центры оснований цилиндра, изображенного на рисунке. Тогда образующей цилиндра является отрезок:
Среди точек
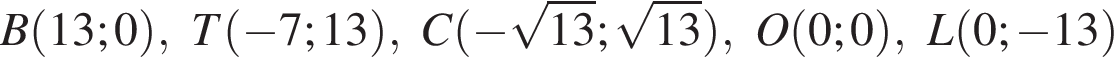 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Найдите значение выражения 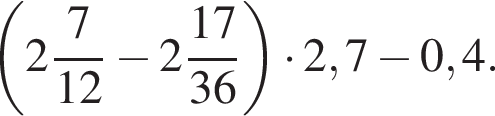
Если 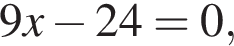 то
то 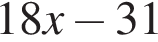 равно:
равно:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что
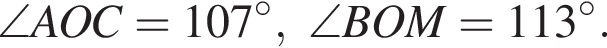 Найдите величину угла BOC.
Найдите величину угла BOC.
Решите неравенство 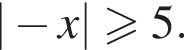
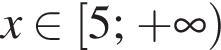


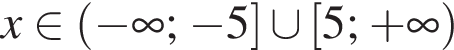
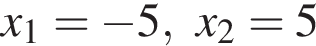
Даны числа: 5100; 0,0051; 5,1 · 10−4; 51 · 103; 0,51 · 105. Укажите число, записанное в стандартном виде.
На координатной плоскости даны точка А, расположенная в узле сетки, и прямая l (см. рис.). Определите координаты точки, симметричной точке А относительно прямой l.
Значение выражения 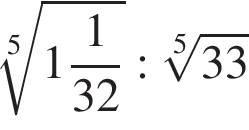 равно:
равно:
Упростите выражение 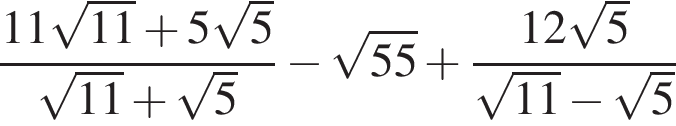
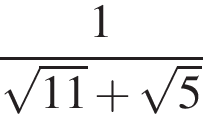 ;
;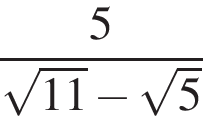 .
.Укажите номер рисунка, на котором представлен эскиз графика функции y = 1 − (x + 3)2.
Параллельно стороне треугольника, равной 5, проведена прямая. Длина отрезка этой прямой, заключенного между сторонами треугольника, равна 2. Найдите отношение площади полученной трапеции к площади исходного треугольника.
Известно, что наименьшее значение функции, заданной формулой y = x2 + 8x + c, равно −3. Тогда значение c равно:
ABCDA1B1C1D1 — куб. Точки M и N — середины ребер AD и DC соответственно, 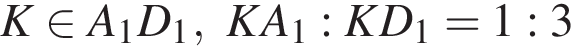 (см. рис.). Сечением куба плоскостью, проходящей через точки M, N и K, является:
(см. рис.). Сечением куба плоскостью, проходящей через точки M, N и K, является:
Расположите числа 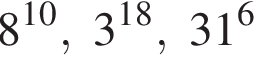 в порядке возрастания.
в порядке возрастания.
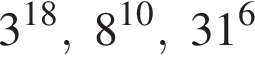
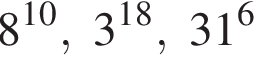
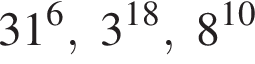
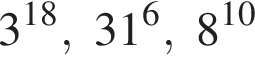
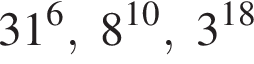
График функции, заданной формулой y = kx + b, симметричен относительно оси Oy и проходит через точку A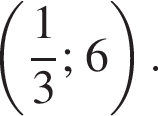 Значение выражения k + b равно:
Значение выражения k + b равно:
Укажите (в градусах) наименьший положительный корень уравнения 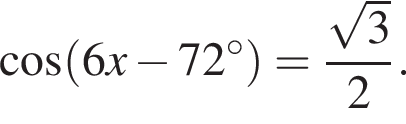
Витя купил в магазине некоторое количество тетрадей, заплатив за них 24 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 2 тетради больше. Сколько тетрадей купил Витя?
Найдите сумму корней (корень, если он единственный) уравнения 
Известно, что при a, равном −2 и 4, значение выражения 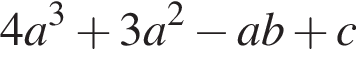 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Найдите сумму наименьшего и наибольшего целых решений неравенства 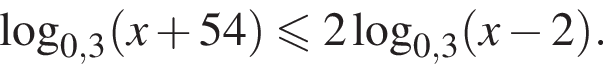
Найдите сумму всех натуральных чисел a, для которых выполняется равенство 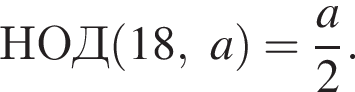
Площадь прямоугольника ABCD равна 20. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Найдите площадь боковой поверхности правильной треугольной пирамиды, если длина биссектрисы ее основания равна ![]() и плоский угол при вершине
и плоский угол при вершине 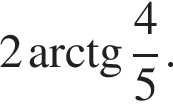
Найдите сумму наименьшего и наибольшего целых решений неравенства 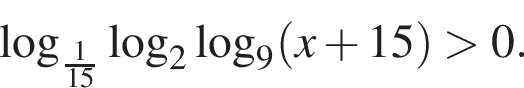
В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с четными номерами на 130 больше суммы членов с нечетными номерами. Найдите сотый член этой прогрессии.
Найдите произведение наименьшего и наибольшего целых решений неравенства 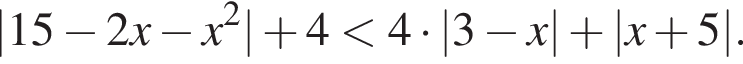
Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
Отрезок BD является биссектрисой треугольника АВС, в котором 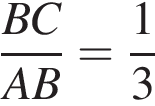 и
и 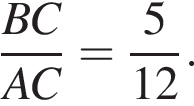 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
Равнобедренная трапеция с основаниями длиной 7 и 3 и острым углом 60° вращается вокруг прямой, содержащей ее боковую сторону. Найдите объем тела вращения V и в ответ запишите значение выражения ![]()

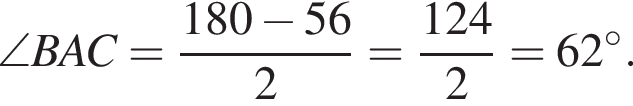
 представляет собой прямую, проходящую через точки вида
представляет собой прямую, проходящую через точки вида 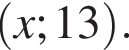 Таким образом, единственное подходящее решение — точка T.
Таким образом, единственное подходящее решение — точка T.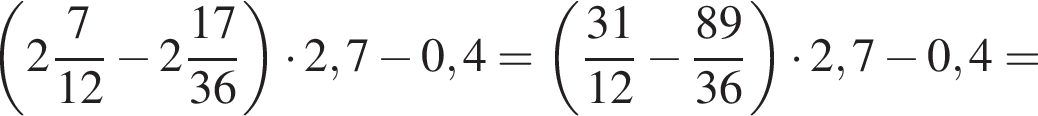
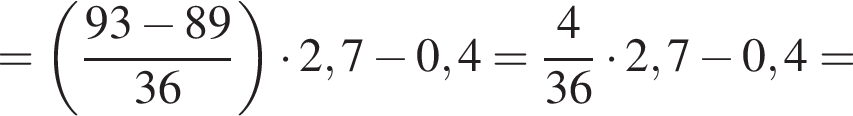
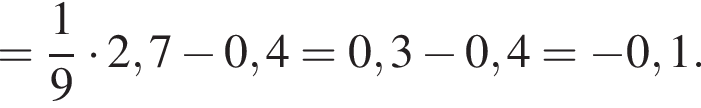
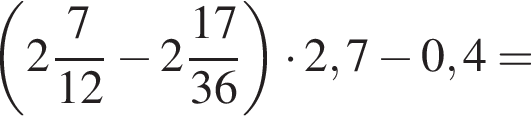
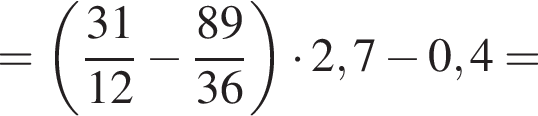
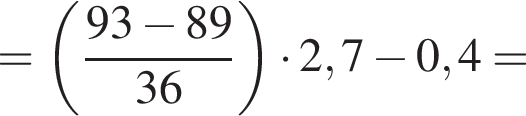
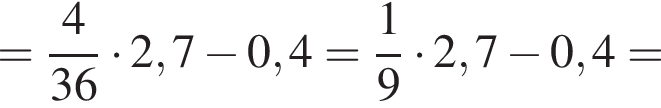
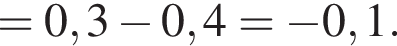
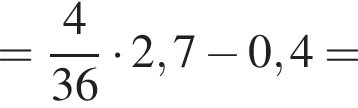
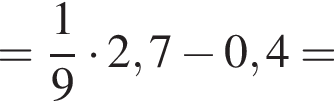
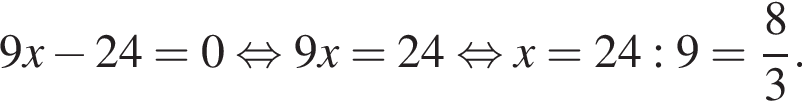
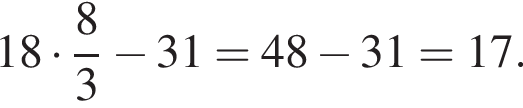
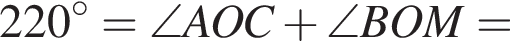

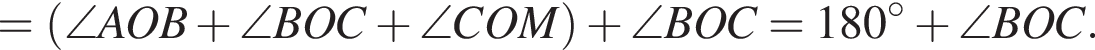




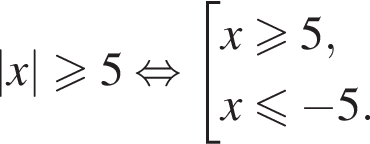
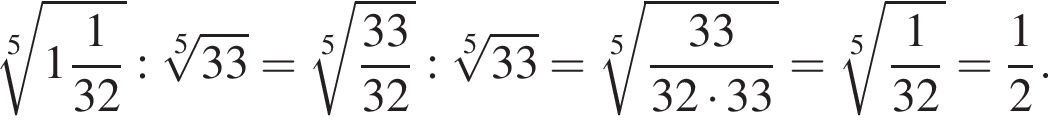
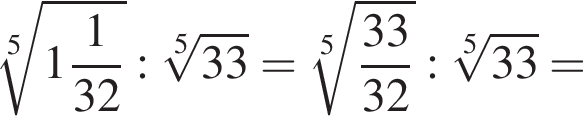
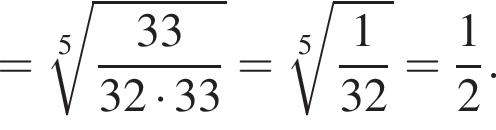
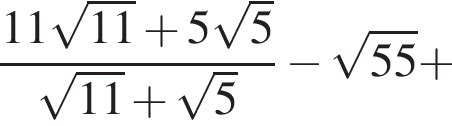
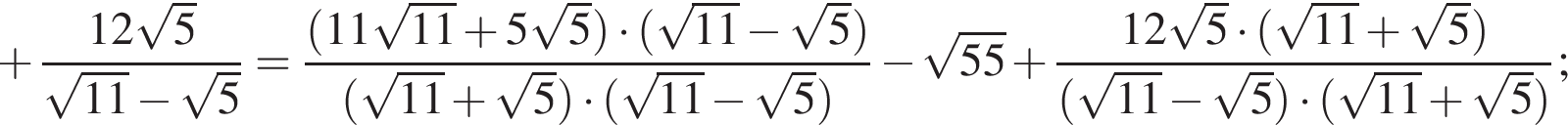
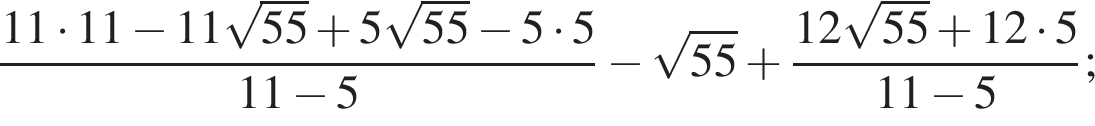
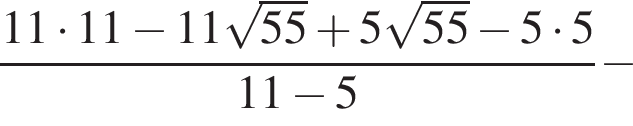
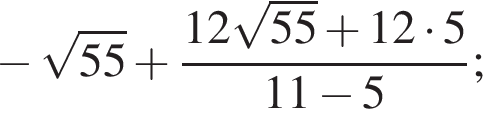
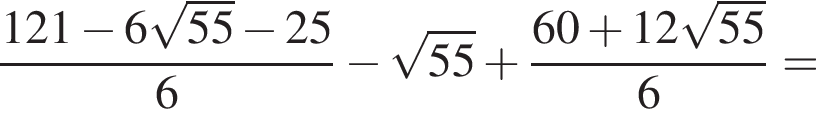
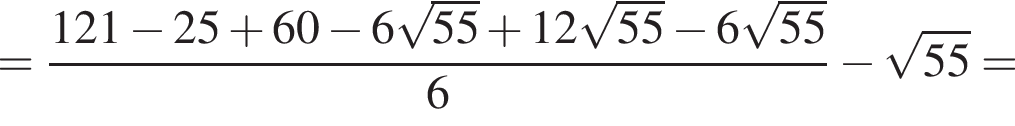

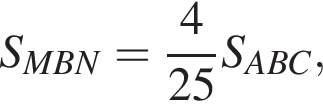 а тогда
а тогда 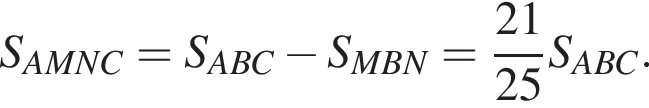
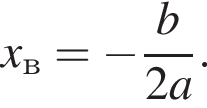 Поэтому
Поэтому 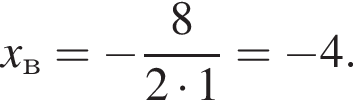 Поскольку y(xв) = −3, имеем:
Поскольку y(xв) = −3, имеем: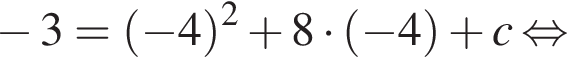

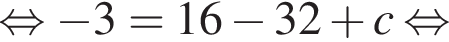
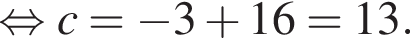
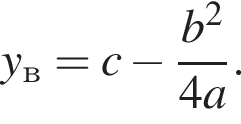
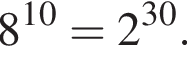 Поскольку все числа положительны, извлечем из каждого корень шестой степени и получим:
Поскольку все числа положительны, извлечем из каждого корень шестой степени и получим: 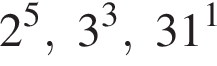 то есть числа 32, 27, 31. Так как 27 < 31 < 32, получаем
то есть числа 32, 27, 31. Так как 27 < 31 < 32, получаем 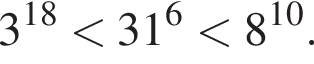
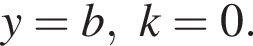 Прямая проходит через точку A с координатами
Прямая проходит через точку A с координатами 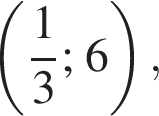 отсюда b = 6. Поэтому k + b = 6.
отсюда b = 6. Поэтому k + b = 6.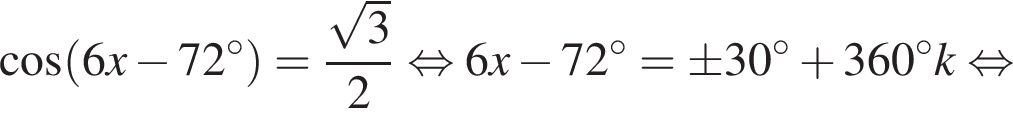
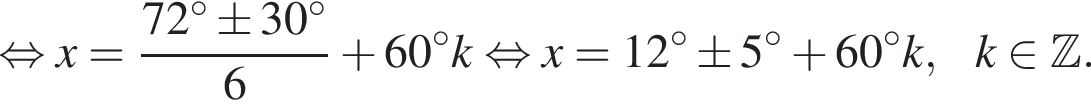
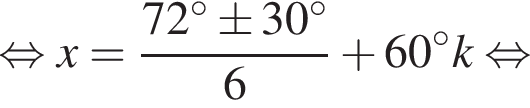

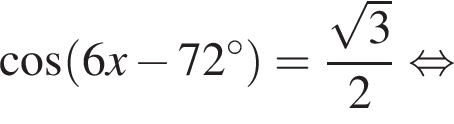

 Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 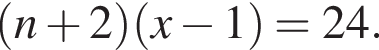 Решим систему уравнений:
Решим систему уравнений: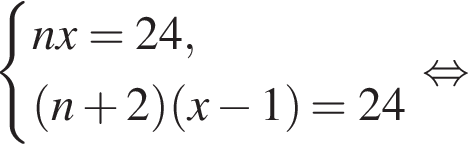
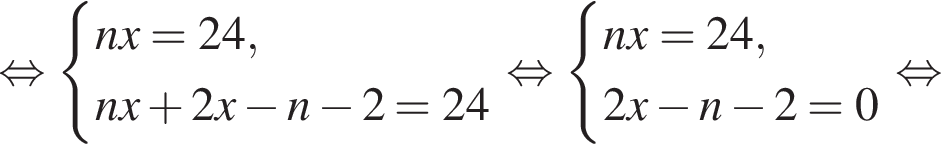
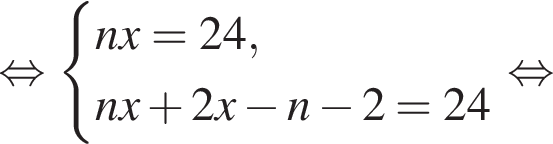
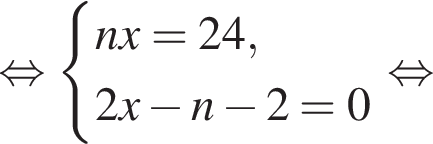
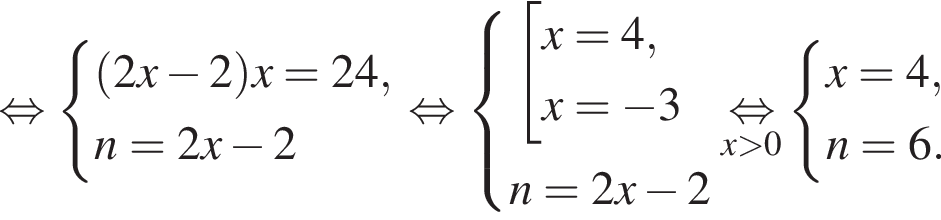
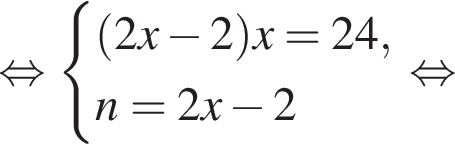
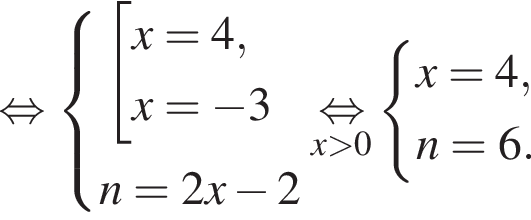
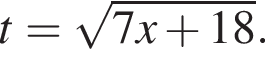 Тогда:
Тогда: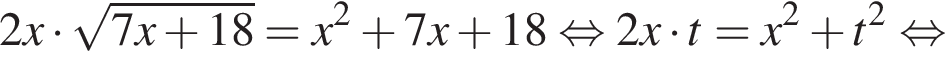

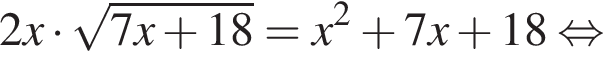


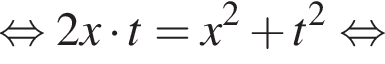
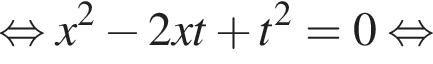
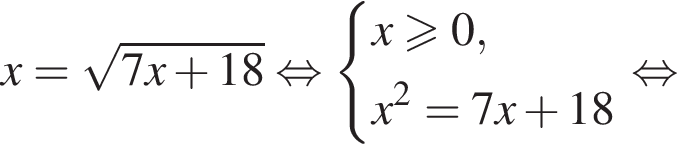
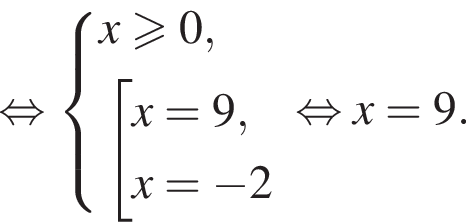
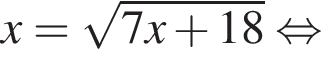
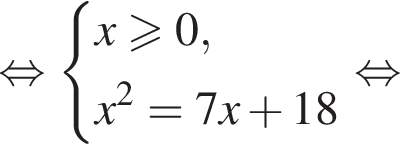
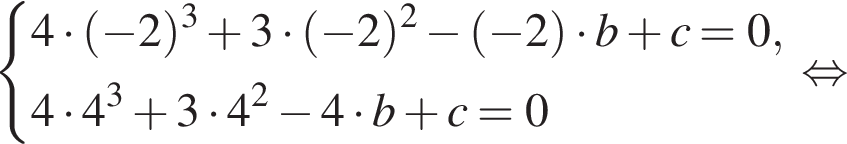
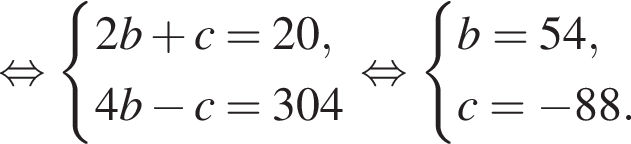
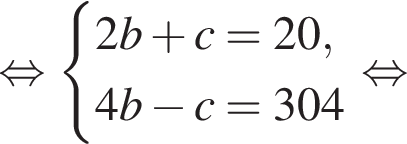
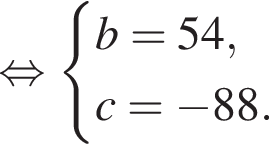

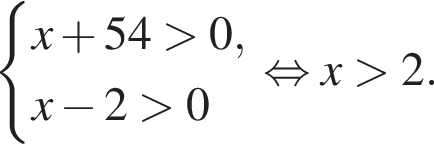
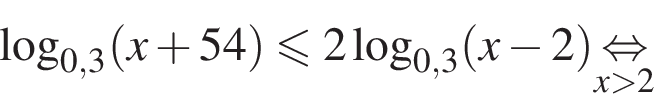
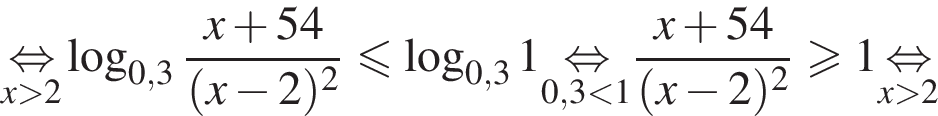
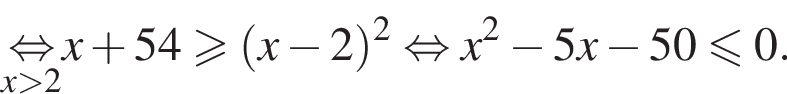
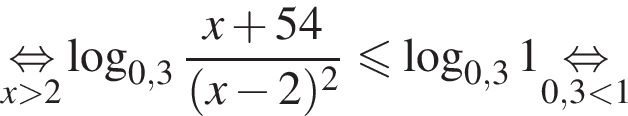
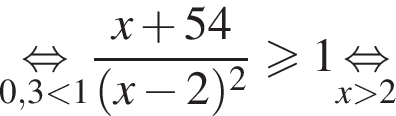

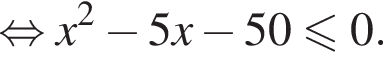
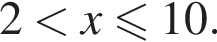 Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.
Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13. Поскольку
Поскольку 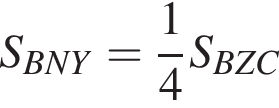 (NY — средняя линия), поэтому
(NY — средняя линия), поэтому 
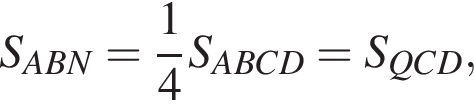 тогда
тогда 

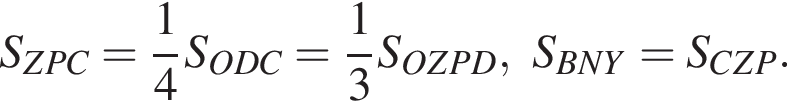
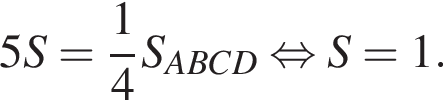
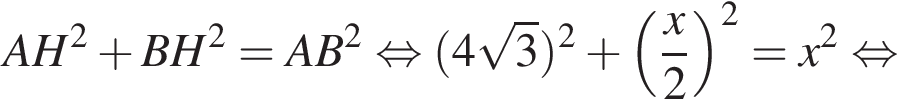
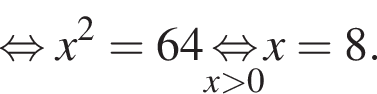
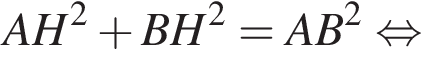
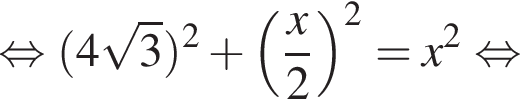
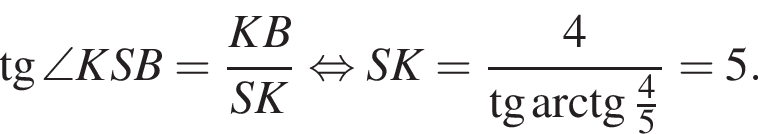 Площадь боковой поверхности равна
Площадь боковой поверхности равна 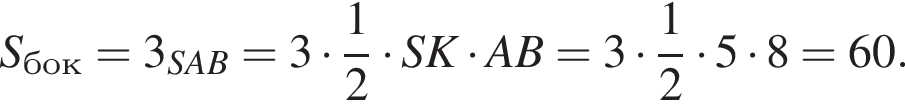
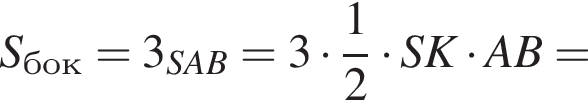
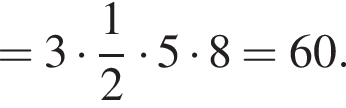
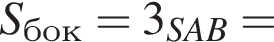
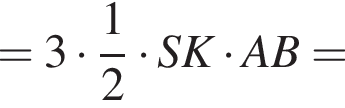
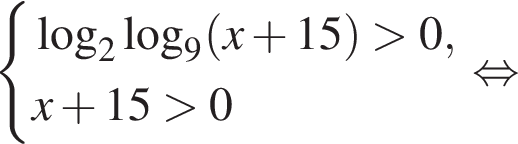
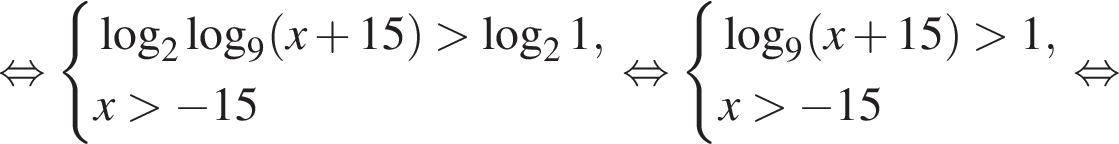
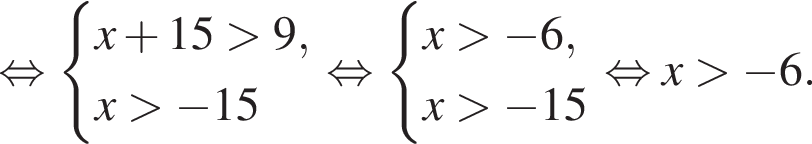
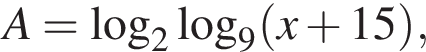 тогда:
тогда: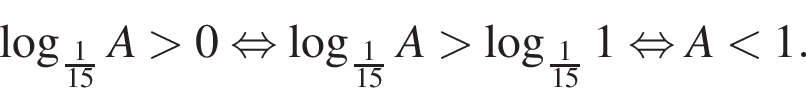
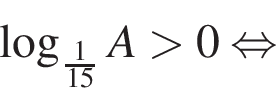
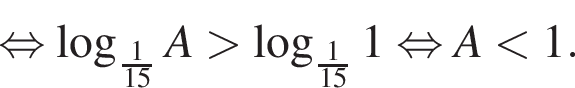

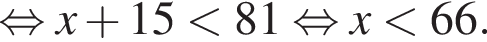


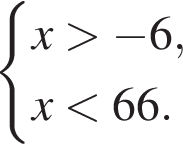 Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.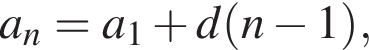 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 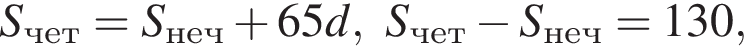 откуда
откуда 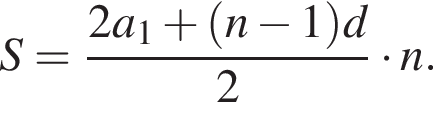 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: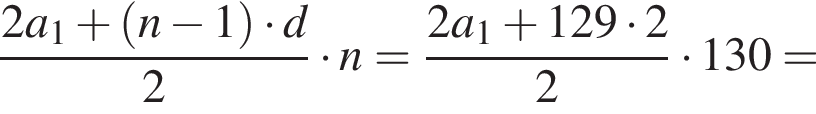
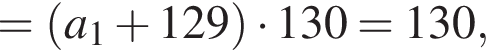
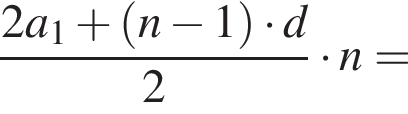
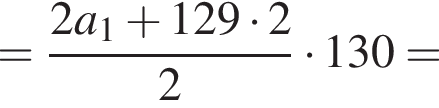
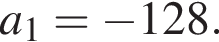 Получим
Получим 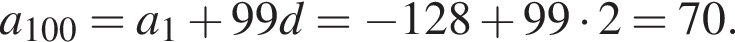
 имеем:
имеем: 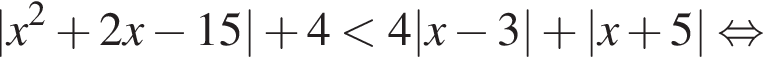
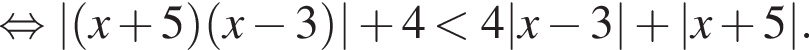
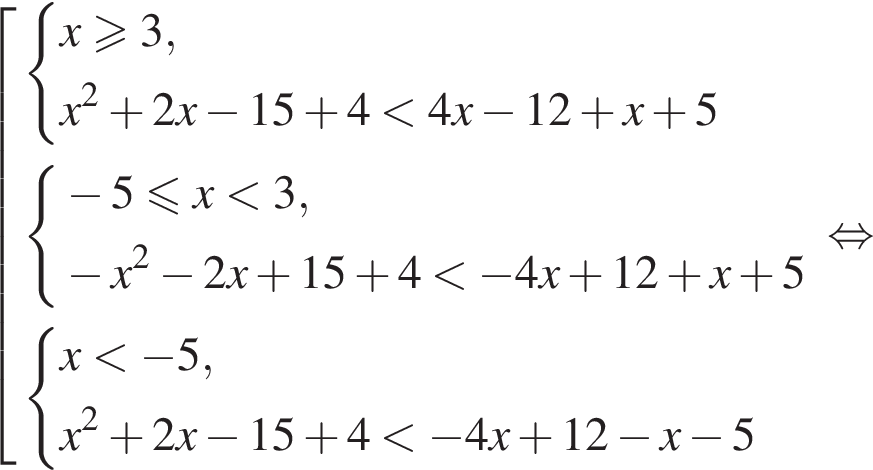
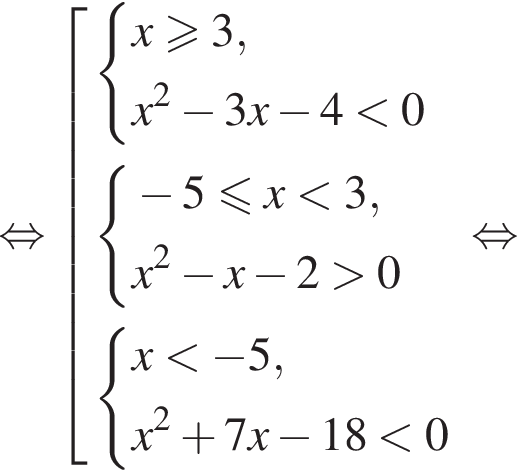
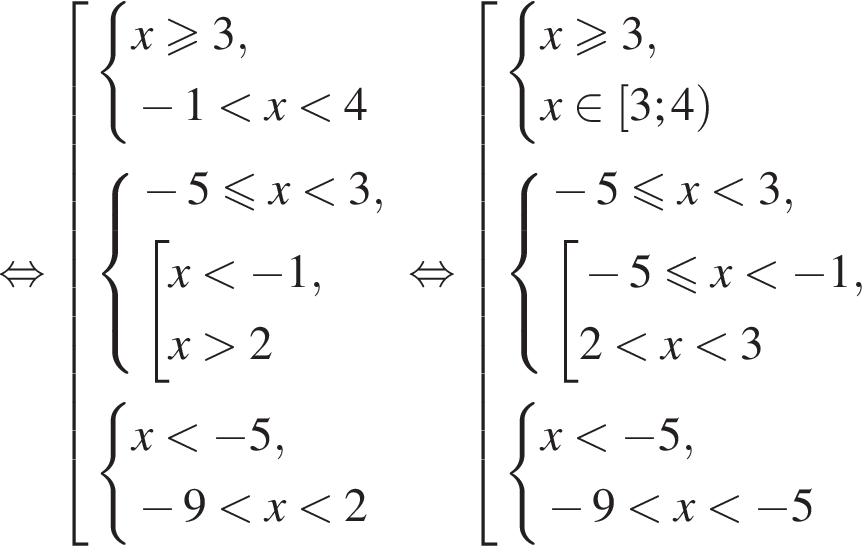
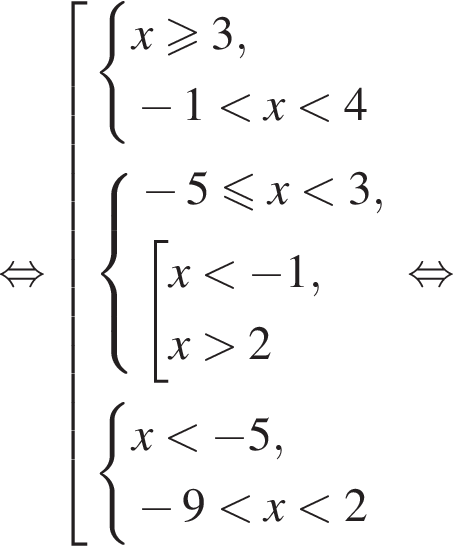
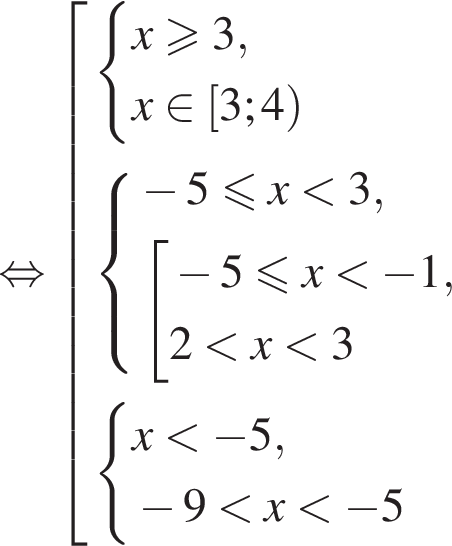
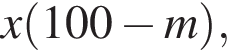 во втором —
во втором — 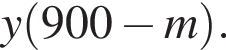 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 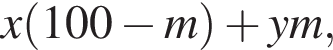 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда: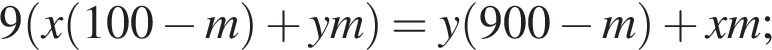
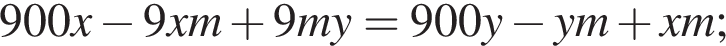

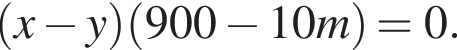

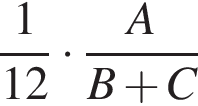 работы.
работы. 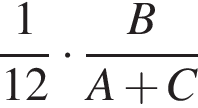 работы.
работы. 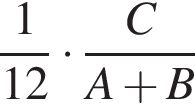 работы.
работы. 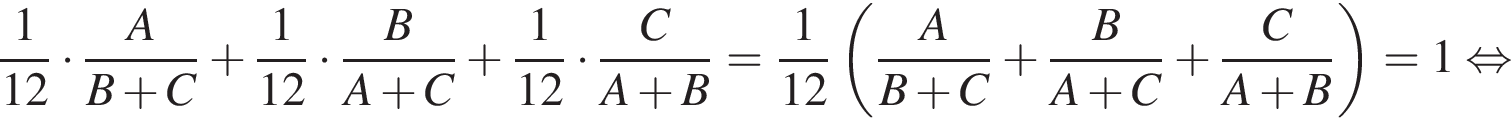
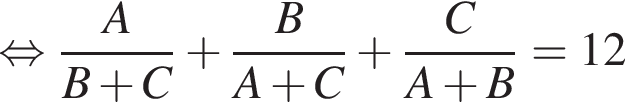
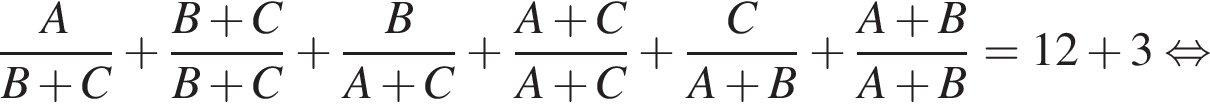
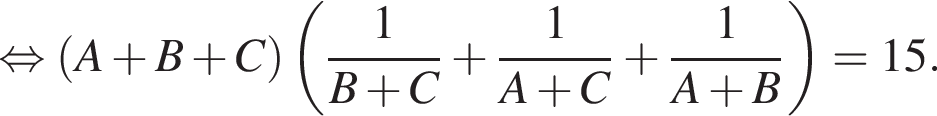
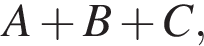 то они выполнили бы работу за:
то они выполнили бы работу за: 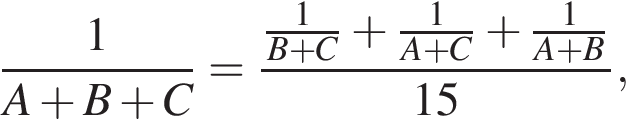
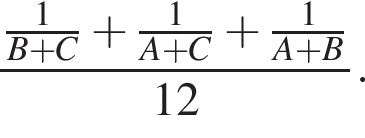 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 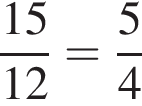 раза быстрее. В ответе будет число
раза быстрее. В ответе будет число 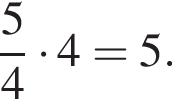
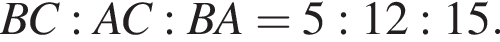 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 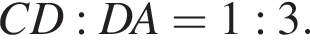 Значит, если
Значит, если  то
то 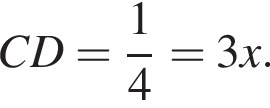
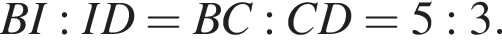 Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что 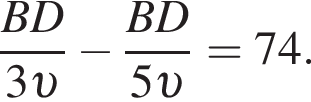
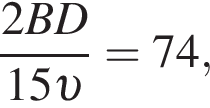 откуда
откуда 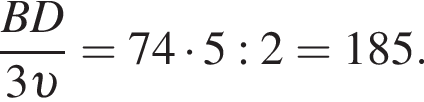
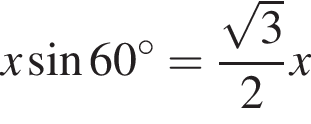 и потому объем двух таких конусов равен
и потому объем двух таких конусов равен